Poliedros
Figuras tridimensionais são figuras a 3 dimensões, ou seja, tem volume. Também são chamadas de "sólidos geométricos". Podemos listar alguns exemplos: a esfera, a pirâmide, o cubo, o cilindro, o cone, os prismas, entre outros.
Sobre os Poliedros
Poliedros são sólidos geométricos formados apenas por polígonos. Portanto, nem a esfera, nem o cone e nem o cilindro são poliedros. Mas o cubo, a pirâmide e os prismas, são.
Um exemplo: cubo:
Podemos planificá-lo da seguinte forma:
E assim vemos que o cubo é formado por 6 quadrados, que são suas faces.
Chamamos "face" cada polígono que forma o poliedro.
Chamamos de "arestas" cada lado dos polígonos ligados entre si.
Chamamos de "vértice" as pontas do poliedro.
Poliedros Platónicos
Os poliedros platónicos são o tetraedro, o cubo, o octaedro, o dodecaedro e o icosaedro: (todos com todas as faces iguais)
O Tetraedro
O tetraedro é um poliedro composto por 4 faces triangulares:
Um tetraedro contém 4 vértices e 6 arestras.
O Cubo
O cubo é um poliedro composto por 6 faces quadradas:
Um cubo contém 8 vértices e 12 arestras.
O Octaedro
O octaedro é um poliedro composto por 8 faces triangulares:
Um octaedro contém 6 vértices e 12 arestras.
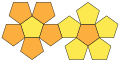
O Dodecaedro
O dodecaedro é composto por 12 faces pentagonais:
Um dodecaedro contém 20 vértices e 30 arestras.
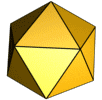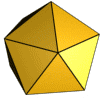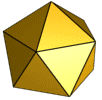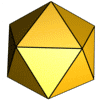
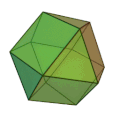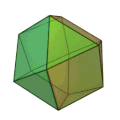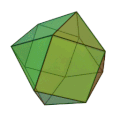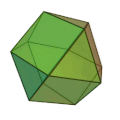
O Icosaedro
O icosaedro é composto por 20 faces triangulares:
Um icosaedro contém 12 vértices e 30 arestras.
Propriedades dos Poliedros Platónicos
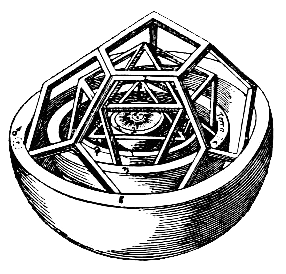
A propriedade que distingue os Poliedros Platónicos de todos os demais é que estes são os únicos sólidos regulares que podem ser inscritos na esfera. Para entender o significado disto, vejamos a inscrição de polígonos num círculo.
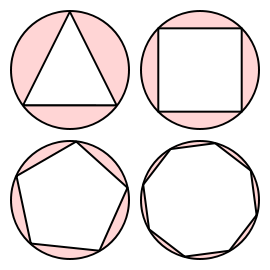
Dizemos que um polígono está inscrito num círculo quando todos vértices do polígono em questão tocam a circunferência deste círculo, isto é, a linha que o delimita.
O fato é que infinitos polígonos regulares (cujos lados tem o mesmo comprimento) podem ser inscritos dentro de um círculo. Alguns exemplos:
O mesmo não acontece com a esfera. Apenas os Poliedros Platónicos são os sólidos regulares (de faces idênticas) que podem ser inscritos nela.
Galeria de Poliedros